Physics 566 Fall 2013

Quantum Optics I

University of New Mexico

Department of Physics and Astronomy

Instructor: Prof. Ivan H. Deutsch

Lectures: Tues. and Thurs. 5:15-6:30 PM, P&A Room 184

Office Hours: Wed. 10:00-11:00, Room 23

Teaching Assistants: Bob Keating and Xiaodong Qi

Problem Session: Mon. 2:00-3:00, Room 5

On this page:

• Map of Quantum Optics
• General Information
• Syllabus
• Lecture Schedule and Notes and Podcasts
• Problem Sets

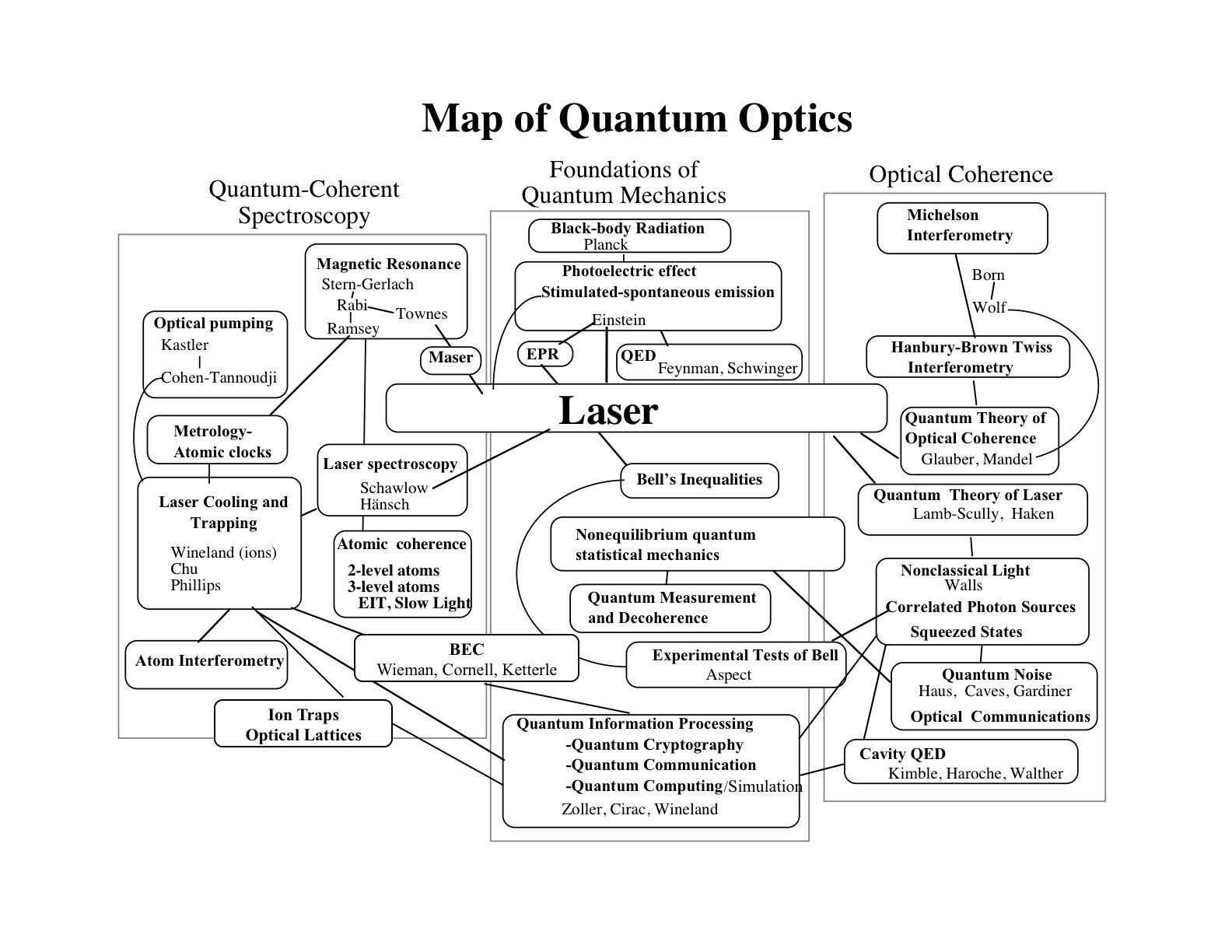
Quantum Optics map (pdf download)

General Information

"Recommended" Texts (none required):

* Atom-Photon interactions- Cohen-Tannoudji,

* Quantum Optics - Scully and Zubairy,

* Quantum Optics, by R. Y. Chiao and J. C. Garrision

We will not be following any of these texts directly . They all have strengths in different areas and are good to have on your bookshelf.

Other Texts:

Recent books (published within the last 5 years)

* Statistical Methods in Quantum Optics 1 and 2, by H. J. Carmichael

* Quantum Noise, by C. Gardiner (also Handbook of Stochastic Methods)

* Quantum Optics, An Introduction, by M. Fox

* Introductory Quantum Optics by C. Gerry and P. Knight

* Fundamental of Quantum Optics, by J. R. Klauder and E. C. G. Sudarshan

* Quantum Optics: Including Noise Reduction, Trapped Ions, Quantum Trajectories, and Decoherence by M. Orszag

* Introduction to Quantum Optics: From Light Quanta to Quantum Teleportation by H. Paul and I. Jex

* Fundamentals of Quantum Optics and Quantum Information by P. Lambropoulos and D. Petrosyan

* Modern Foundations Of Quantum Optics by Vlatko Vedral

Older standards

* Elements of Quantum Optics, by P. Meystre and M. Sargent

"Quantum Optics" - Walls and Milburn

* Photons and Atoms: Introduction to Quantum Electrodynamics, by Claude Cohen-Tannoudji et al.

* Optical Coherence and Quantum Optics, by L. Mandel and E. Wolf

* Lasers, by P. Milonni and J. H. Eberly

* Optical Resonance and Two-Level Atoms , by Allen and J. H. Eberly

* Quantum Statistical Properties of Radiation, by W. H. Louisell

* Quantum Properties or Radiation, R. Loudon

* Laser Theory, by H. Haken

Grading:

* Problem Sets (8-10 assignments) 50%

* Midterm 25%

* Final Project 25%

* Problem sets will be available on the web, about every week. Generally assignments will be due in class, Tuesdays.

Tentative Syllabus

Phys. 566: Quantum Optics I

I. Classical foundations

            A. Oscillators, interference, and coherence.

            B. Simple harmonic oscillators, quadratures, and Fourier analysis.

            C. Lorentz oscillator model.

 

II. Quantum foundations

            A. Density matrix and coherence.

            B. Two level systems -- Pauli algebra, Bloch-sphere, magnetic resonance.

            C. Quantum simple harmonic oscillator.

 

III. Optical resonance for two level atoms

            A. Atom-photon interaction in electric dipole approximation.

            B. Pseudo-spin formulation, Rabi flopping.

            C. Density matrix formulation.

            D. Phenomenological damping -- master equation and rate equations.

 

IV. The electromagnetic vacuum

            A. Quantization of the electromagnetic field.

            B. Spontaneous emission and Wigner-Weisskopf theory.

            C. Resonance fluorescence -- Mollow triplet.

            D. Jaynes-Cummings model -- Dressed states.

 

V. Three level quantum coherence

            A. Raman resonance.

            B. Dark states and EIT.

            C. Slow light, fast light, and polaratons.

 

VI. Quantum-Optical Coherence

            A. Photon counting statistics -- Mandel's formula.

            B. Theory of partial coherence - Classical statistical optics

            C. Coherent states as quasi-classical states.

            D. Glauber's correlation functions.

            E. Hanbury-Brown and Twiss interferometry.

            F. Bunching, antibunching ,and photon statistics.
 

 

Phys. 581: Quantum Optics II

I. Nonclassical Light

            A. Phase space methods -- Quasiprobability distributions, P-Glauber, Q-Husimi, W-Wigner functions.

            B. Nonlinear optics and nonclassical light.

            C. Squeezed states.

            D. Homodyne detection.

            E. Correlated twin photons.

            F. Photon interferometry.

II. Foundations

            A. Bipartite entanglement.

            B. EPR and Bell’s Inequalities, finite and infinite dimensional systems.

            C. Completely-positive map, Kraus operators, and POVMs.

 

III. Open quantum systems

            A. System-reservoir interactions.

            B. Born-Markoff approximation and the Lindblad Master Equation.

            C. Phase-space representation:  Fokker-Planck equation.

            D. Heisenberg-Langevin equation.

 

III. Continuous measurement

            A. Quantum trajectories – different unravelings of the Master Equation.

            B. Quantum Monte-Carlo wave functions.

            C. The stochastic Schrödinger equation.

            D. Quantum filtering theory.

 

IV. Fundamental Paradigms of quantum optics

            A. Cavity QED (from atoms to superconductors)

            B. Ion traps.

            C. Cold neutral atom ensembles.

            D. Correlated photons and squeezed states.

 

V. Applications in quantum information processing

            A. Quantum communication

            B. Quantum computation

            C. Quantum metrology

Problem Sets

Final Project