

Office Hours: Mon. 11-12, PandA Room 24
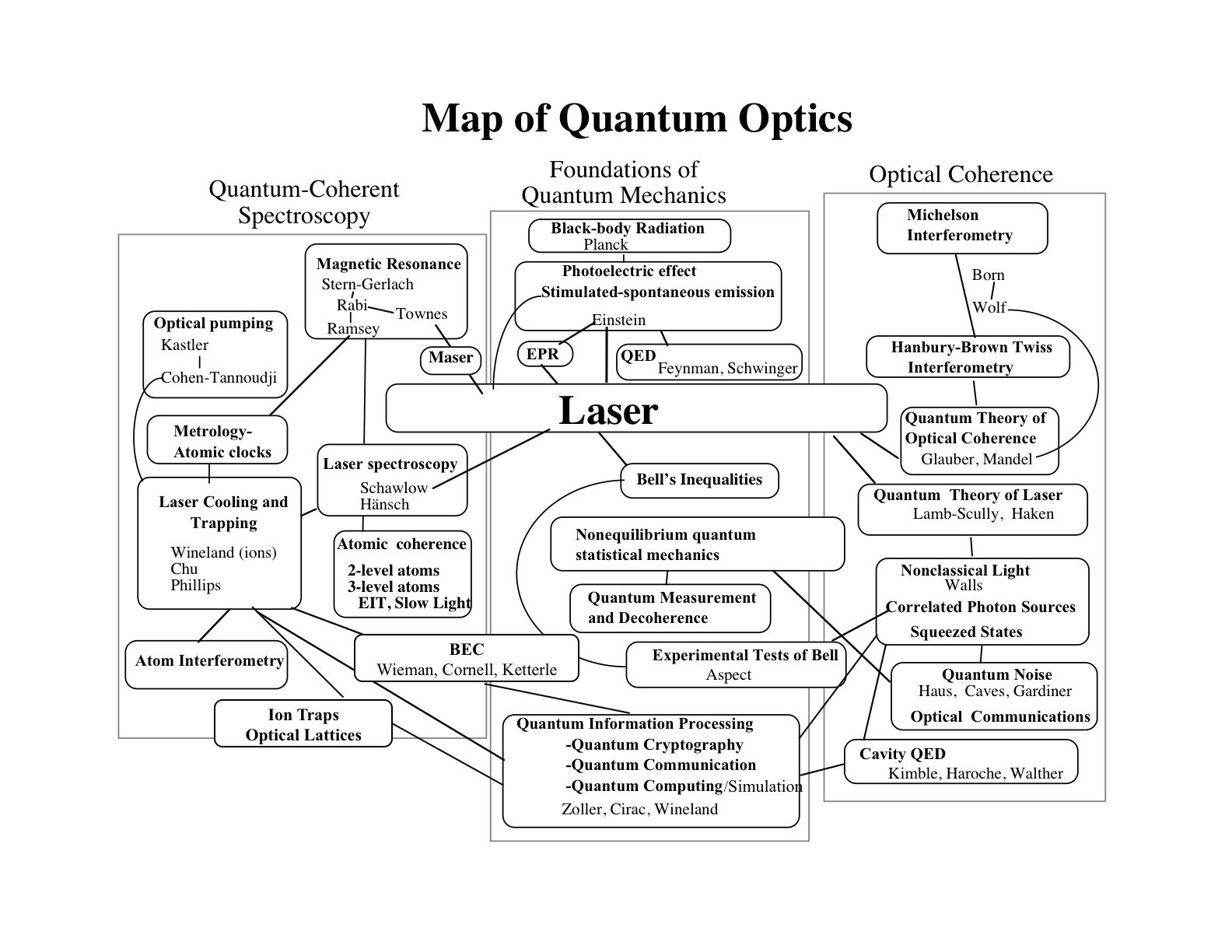
Quantum Optic map (pdf download)
"Recommended" Texts:
* "Atom-Photon interactions"- Cohen-Tannoudji,
* "Quantum Optics" - Scully and Zubairy,
* "Quantum Optics" - Walls and Milburn
We will not be following any of these texts directly . They all have strengths in different areas and are good to have on your bookshelf.
Other Texts:
Recent books (published within the last 5 years)
* Statistical Methods in Quantum Optics 1 and 2, by H. J. Carmichael
* Quantum Optics, by R. Y. Chiao and J. C. Garrision
* Quantum Noise, by C. Gardiner (also Handbook of Stochastic Methods)
* Introductory Quantum Optics by C. Gerry and P. Knight
* Fundamental of Quantum Optics, by J. R. Klauder and E. C. G. Sudarshan
* Quantum Optics: Including Noise Reduction, Trapped Ions, Quantum Trajectories, and Decoherence by M. Orszag
* Introduction to Quantum Optics: From Light Quanta to Quantum Teleportation by H. Paul and I. Jex
* Fundamentals of Quantum Optics and Quantum Information by P. Lambropoulos and D. Petrosyan
* Modern Foundations Of Quantum Optics by Vlatko Vedral
Older standards
* Elements of Quantum Optics, by P. Meystre and M. Sargent
* Photons and Atoms: Introduction to Quantum Electrodynamics, by Claude Cohen-Tannoudji et al.
* Optical Coherence and Quantum Optics, by L. Mandel and E. Wolf
* Lasers, by P. Milonni and J. H. Eberly
* Optical Resonance and Two-Level Atoms , by Allen and J. H. Eberly
* Quantum Statistical Properties of Radiation, by W. H. Louisell
* Quantum Properties or Radiation, R. Loudon
* Laser Theory, by H. Haken
Grading:
* Problem Sets (8-10 assignments) 50%
* Take Home Midterm 25%
* Final Project 25%
* Problem sets will be available on the web, about every week. Generally assignments will be due in my mailbox by 5:00 Fridays.
I Foundations
A. Review of Quantum Mechanics: Hilbert space, operators, states, time evolution.
B. Two level systems - Pauli algebra, Bloch-sphere, magnetic resonance.
C. Simple Harmonic Oscillator.
II. Optical resonance for two level atoms
A. Atom-photon interaction in electric dipole approximation.
B. Pseudo-spin formulation, Rabi flopping.
C. Density matrix formulation.
D. Phenomenological damping - master equation and rate equations.
IV. The electromagnetic vacuum
A. Quantization of the electromagnetic field.
B. Spontaneous emission.
C. Resonance fluorescence -- Mollow triplet
VI Nonclassical light
A. Photon counting statistics -- Mandel's formula.
B. Coherent states as quasi-classical states.
C. Phase space methods - Quasiprobability distributions, P,Q, Wigner functions.
D. Squeezed states.
E. Theory of partial coherence -- Glauber's correlation functions.
F. Photon antibunching and resonance fluorescence.
G. Jaynes-Cummings model -- Dressed states, collapse and revival.
V Theory of dissipation in quantum mechanics
A. System reservoir interaction.
B. Derivation of the Linblad master equation in the Born-Markov approximation.
C. Damped two-level atom and simple harmonic oscillators.
D. Heisenberg formulation - Langevin equations.
VII Theoretical methods for open quantum systems
A. Formal theory of the density operators.
B. Quantum trajectories -- Unraveling the master equation.
C. Measurement theory and decoherence.
Problem Set #1
|
Problem Set #5
|
Problem Set #2
|
Problem Set #6
|
Problem Set #3
|
Problem Set #7
|
Problem Set #4
|
Problem Set #8
|
As a final project for the class, you will review an experiment in quantum optics anbd describe theory behind it. The goal is to understand how the particular system works and the physics that is explored in the experiment. Possible topics are shown below. Your topic must meet my approval.
Target Dates:
- Submission of abstract of project: Nov.11
- Approval: Nov.13
- Due Dec. 15
Format:
- Submission as if for publication to Physical Review A: 5-8 double column Physical Review pages.
- All styles STRICTLY according to APS style guidelines. http://authors.aps.org/STYLE/.
- Manuscript preparation is described here: http://authors.aps.org/INFOAUTH/msprep.html.
- File formats are described here: http://authors.aps.org/esubs/guidelines.html#fileformat.
- The Physical Review provides LaTex templates in a macro called "RevTex": http://authors.aps.org/revtex4/ .
- Submission to me, by email (ideutsch@unm.edu) in PDF ONLY-- tex, dvi, ps, MS word, NOT accepted.
Suggested Topics
A. Laser spectroscopy
1. Electromagnetically Induced Transparency (EIT).
2. Lasing without inversion.
3. "Fast" and "slow" light.
B. Atom cooling and trapping
1. Ion traps
2. Optical Molasses and Magneto-Optic Trap (MOT).
3. Optical lattices.
4. Atom interferometry.
C. Cavity QED
1. Microwaves and Rydberg atoms.
2. Optical Cavity QED.
3. Modification of spontaneous emission for atoms in cavities.
4. VCELS and cavity QED in solids.
5. Micromasers (with atoms) / microlasers (in solids).
D. Nonclassical light
1. Photon anti bunching and resonance fluorescence.
2. Production of squeezed states via four-wave mixing, parametric oscillation,
second harmonic generation.
3. Correlated two-photon production via parametric downconversion.
4. Interferometry below the standard quantum limt.,
5. Optical paramteric oscillator.
6. Large spin systems as continuous variable quantum systems
E. Spin systems
1. Spin squeezing and interferometry.
2. Polarization spectroscopy and spin control.
3. Large spin ensembles as continuous variable systems.
F. Quantum Information Processing
1. Nonclassical atomic motion engineering with trapped ions.
2. Quantum memory using atomic ensembles.
2. Quantum computing: Ions, Atoms, Linear/Nonlinear Optics.
3. Quantum cryptography.
4. Quantum teloportation.
G. Quantum Measurement Foundations
1. Quantum nondemolition measurement.
2. Entanglement: Bells Inequalities, Discrete variables, Continuous variables.
3. Quantum jumps and the "Quantum Zeno Effect".
4. Quantum state tomography and state measurement.
5. Continuous measurement and quantum feedback.
6. Decoherence and the quantum-classical transition - theory and experiment.
Final Project Publication
Electronic
Journal - Reviews of Quantum Optics, Vol. 1, 1999