(Tues. and Thurs. 5:30-6:45, PandA Room 5)
Office Hours: MW 11:00-12:00, PandA room 24

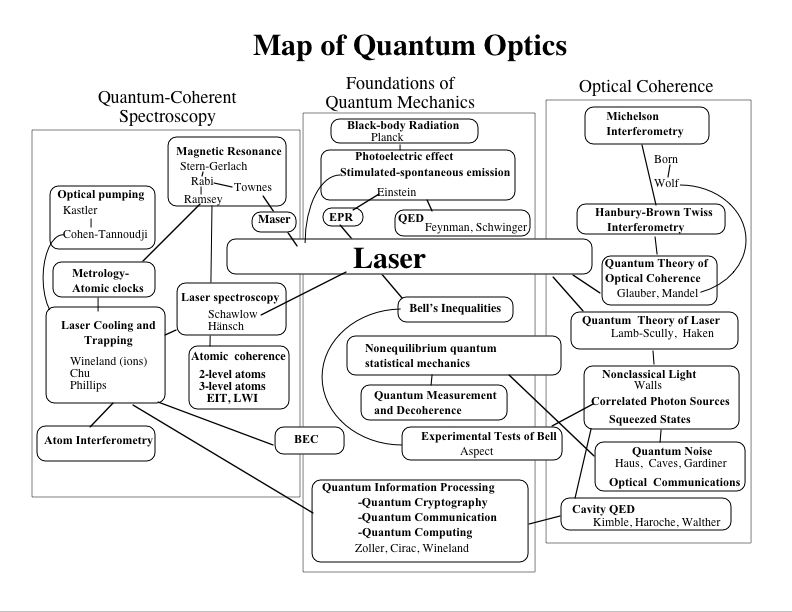
Quantum Optic map (pdf download)
"Recommended" Texts:
* "Atom-Photon interactions"- Cohen-Tannoudji,
* "Quantum Optics" - Scully and Zubairy,
* "Quantum Optics" - Walls and Milburn
We will not be following any of these texts directly . They all have strengths in different areas and are good to have on your bookshelf.
Other Texts:
Recent books (published within the last ten years)
* Elements of Quantum Optics, by P. Meystre and M. Sargent
* Photons and Atoms: Introduction to Quantum Electrodynamics,
by Claude Cohen-Tannoudji et al.
* Optical Coherence and Quantum Optics, by L. Mandel and E. Wolf
* Lasers, by P. Milonni and J. H. Eberly
* Quantum Noise, by C. Gardiner (also Handbook of Stochastic Methods)
* Statistical Methods in Quantum Optics 1, by H. J. Carmichael
Old standards
* Optical Resonance and Two-Level Atoms , by Allen and J. H. Eberly
* Quantum Statistical Properties of Radiation, by W. H. Louisell
* Quantum Properties or Radiation, R. Loudon
* Laser Theory, by H. Haken
Grading:
· Problem Sets (7 assignments) 70%
· Final Projects 30%
· Problem sets will be available on the web, about every week. Generally assignments will be due in class Thursdays.
I Foundations
A. Review of Quantum Mechanics: Hilbert space, operators, states, time evolution.
B. Two level systems - Pauli algebra, Bloch-sphere, magnetic resonance.
C. Simple Harmonic Oscillator.
II. Optical resonance for two level atoms
A. Atom-photon interaction in electric dipole approximation.
B. Pseudo-spin formulation, Rabi flopping.
C. Density matrix formulation.
D. Phenomenological damping - master equation and rate equations.
IV. The electromagnetic vacuum
A. Quantization of the electromagnetic field.
B. Spontaneous emission.
C. Resonance fluorescence -- Mollow triplet
VI Nonclassical light
A. Photon counting statistics -- Mandel's formula.
B. Coherent states as quasi-classical states.
C. Phase space methods - Quasiprobability distributions, P,Q, Wigner functions.
D. Squeezed states.
E. Theory of partial coherence -- Glauber's correlation functions.
F. Photon antibunching and resonance fluorescence.
G. Jaynes-Cummings model -- Dressed states, collapse and revival.
V Theory of dissipation in quantum mechanics
A. System reservoir interaction.
B. Derivation of the Linblad master equation in the Born-Markov approximation.
C. Damped two-level atom and simple harmonic oscillators.
D. Heisenberg formulation - Langevin equations.
VII Theoretical methods for open quantum systems
A. Formal theory of the density operators.
B. Quantum trajectories -- Unraveling the master equation.
C. Measurement theory and decoherence.
VIII Experimental paradigms
A. Cavity QED
B. Ion Traps
C. Optical Lattices
D. Parametric down conversion and correlated photon interferometry
Problem Set #1 |
Problem Set #5 |
Problem Set #2 |
Problem Set #6 |
Problem Set #3 |
Problem Set #7 |
Problem Set #4 |
Problem Set #8 |
As a final project for the class, you will review an experiment in quantum optics. The goal is to understand how the particular system works and the physics that is explored in the experiment. Possible topics are shown below. Your topic must meet my approval.
Target Dates:
- Submission of abstract of project: Nov. 4
- Approval: Nov. 5
- Due Dec. 7
TOPICS
A. Laser spectroscopy
1. Electromagnetically Induced Transparency (EIT).
2. Lasing without inversion.
3. "Fast" and "slow" light.
B. Atom cooling and trapping
1. Ion traps
2. Optical Molasses and Magneto-Optic Trap (MOT).
3. Optical lattices.
4. Atom interferometry.
C. Cavity QED
1. Microwaves and Rydberg atoms.
2. Optical Cavity QED.
3. Modification of spontaneous emission for atoms in cavities.
4. VCELS and cavity QED in solids.
5. Micromasers (with atoms) / microlasers (in solids).
D. Nonclassical light
1. Photon anti bunching and resonance fluorescence.
2. Production of squeezed states via four-wave mixing, parametric oscillation,
second harmonic generation.
3. Correlated two-photon production via parametric downconversion.
E. Quantum Information Processing
1. Nonclassical atomic motion engineering with trapped ions.
2. Quantum computing with trapped ions.
3. Quantum computing with cavity QED.
4. Quantum computing in optical lattices.
5. Quantum state tomography and state measurement.
F. Quantum Measurement Foundations
1. Quantum nondemolition measurement.
2. Quantum jumps and the "Quantum Zeno Effect".
3. Continuous measurement and quantum feedback.
4. Decoherence and the quantum-classical transition - theory and experiment.
Final Project Publication
Electronic Journal - Reviews of Quantum Optics, Vol. 1, 1999