

Office Hours: Fridays 11-12, room 23
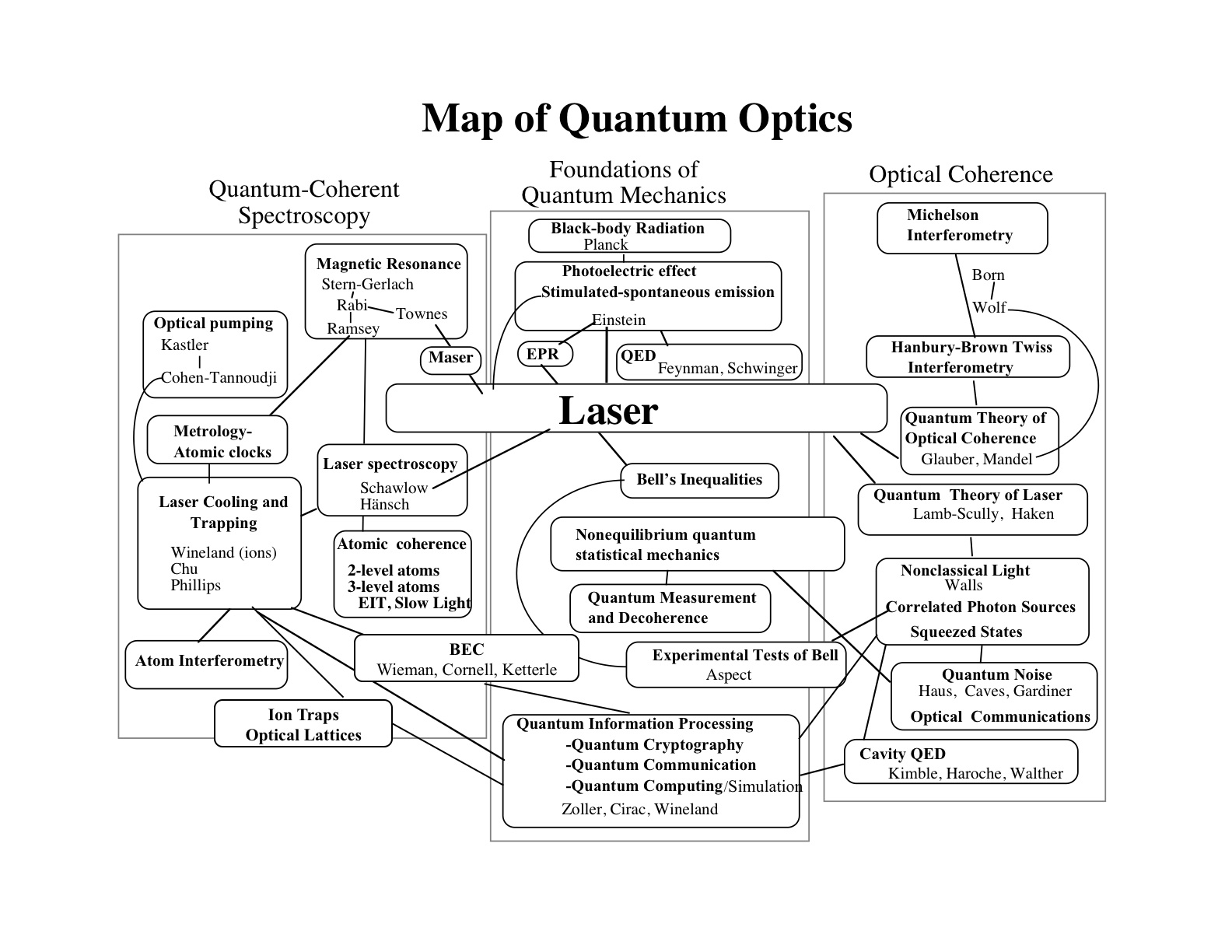
Quantum Optic map (pdf download)
"Recommended" Texts (none required):
* "Atom-Photon interactions"- Cohen-Tannoudji,
* "Quantum Optics" - Scully and Zubairy,
* "Quantum Optics" - Walls and Milburn
We will not be following any of these texts directly . They all have strengths in different areas and are good to have on your bookshelf.
Other Texts:
Recent books (published within the last 5 years)
* Statistical Methods in Quantum Optics 1 and 2, by H. J. Carmichael
* Quantum Optics, by R. Y. Chiao and J. C. Garrision
* Quantum Noise, by C. Gardiner (also Handbook of Stochastic Methods)
* Introductory Quantum Optics by C. Gerry and P. Knight
* Fundamental of Quantum Optics, by J. R. Klauder and E. C. G. Sudarshan
* Quantum Optics: Including Noise Reduction, Trapped Ions, Quantum Trajectories, and Decoherence by M. Orszag
* Introduction to Quantum Optics: From Light Quanta to Quantum Teleportation by H. Paul and I. Jex
* Fundamentals of Quantum Optics and Quantum Information by P. Lambropoulos and D. Petrosyan
* Modern Foundations Of Quantum Optics by Vlatko Vedral
Older standards
* Elements of Quantum Optics, by P. Meystre and M. Sargent
* Photons and Atoms: Introduction to Quantum Electrodynamics, by Claude Cohen-Tannoudji et al.
* Optical Coherence and Quantum Optics, by L. Mandel and E. Wolf
* Lasers, by P. Milonni and J. H. Eberly
* Optical Resonance and Two-Level Atoms , by Allen and J. H. Eberly
* Quantum Statistical Properties of Radiation, by W. H. Louisell
* Quantum Properties or Radiation, R. Loudon
* Laser Theory, by H. Haken
Grading:
* Problem Sets (8-10 assignments) 50%
* Take Home Midterm 25%
* Final Project 25%
* Problem sets will be available on the web, about every week. Generally assignments will be due in Leigh Norris's mailbox at 3:00 PM Fridays.
I Foundations
A. Review of Quantum Mechanics: Hilbert space, operators, states, time evolution.
B. Two level systems - Pauli algebra, Bloch-sphere, magnetic resonance.
C. Simple Harmonic Oscillator.
II. Optical resonance for two level atoms
A. Atom-photon interaction in electric dipole approximation.
B. Pseudo-spin formulation, Rabi flopping.
C. Density matrix formulation.
D. Phenomenological damping - master equation and rate equations.
IV. The electromagnetic vacuum
A. Quantization of the electromagnetic field.
B. Spontaneous emission.
C. Resonance fluorescence -- Mollow triplet
VI Nonclassical light
A. Photon counting statistics -- Mandel's formula.
B. Coherent states as quasi-classical states.
C. Phase space methods - Quasiprobability distributions, P,Q, Wigner functions.
D. Squeezed states.
E. Theory of partial coherence -- Glauber's correlation functions.
F. Photon antibunching and resonance fluorescence.
G. Jaynes-Cummings model -- Dressed states, collapse and revival.
V Theory of dissipation in quantum mechanics
A. System reservoir interaction.
B. Derivation of the Linblad master equation in the Born-Markov approximation.
C. Damped two-level atom and simple harmonic oscillators.
D. Heisenberg formulation - Langevin equations.
VII Theoretical methods for open quantum systems
A. Formal theory of the density operators.
B. Quantum trajectories -- Unraveling the master equation.
C. Measurement theory and decoherence.
| Aug. 24 |
Overview of Class: Review of Quantum mechanics |
|
Aug.
26 |
The Density Matrix |
|
Aug. 31 |
Two level systems - Paul algebra, Bloch-sphere |
|
Sep. 2 |
Magnetic Resonance - Rabi flopping (I) |
|
Sep. 7 |
Magnetic Resonance - Rabi flopping (II) |
Continuation Lect 3 |
Sep.
9 |
Optical Bloch Equations (I) Laser spectroscopy as magnetic resonance |
|
Sep. 14 |
Optical Bloch Equations (II) Phenomenological decay T1 and T2 |
|
Sep.
16 |
Optical Bloch Equations (III) Two-level Atomic Response |
|
Sep. 21 |
Introduction to Quantum Field Theory |
|
Sep. 23 |
Introduction to Quantum Field Theory (Ii) |
|
Sep. 28 |
Quantization of the electromagnetic
field |
|
| Sep. 30 |
Spontaneous
emission: Wigner-Weisskopf |
|
Oct.
5 |
Are there photons? Photon counting experiments and photon statistics |
|
Oct.7 |
Coherent states as quasiclassical states |
|
Oct.
12 |
Phase space methods in Quantum Mechanics |
|
Oct. 14 |
Fall Break |
|
Oct.19
|
Wigner,
Glauber-P, Q functions |
|
Oct. 21 |
Interferometry and coherence: Hanbury-Brown Twiss |
|
Special Supplement: Glauber Les Houches Lectures (1964) - "Quantum Theory of Coherence" |
||
| Oct. 26 |
Glauber correlation functions: Optical coherence and photon statistics |
|
| Oct. 28 |
Nonclassical Light: Photon Antibunching, Resonance fluorescence |
|
Nov. 2 |
Nonlinear Optics and Nonclassical Light: Parametric Downconversion and two-photon interferometry |
|
Nov.
4 |
Squeezed states - General properties |
|
Nov.
9 |
Squeezed states - Production and detection |
|
| Nov. 11 |
Interaction of atoms and quantized field - Jaynes Cummings vs. irreversable |
|
| Nov. 16 |
Open Quantum Systems Tensor products, marginal density opertor, entanglement |
|
Nov.
18 |
Quantum Opertations, POVMs, Krause representation |
|
Nov. 22 Make Up |
Irreverisble bipartite system-reservoir interaction. Markov approximation - Lindblad Master Equation |
|
Nov. 23 |
Examples of Master Equation Evolution: Damped two-level atom, damped SHO |
|
Nov.
25 |
Thanksgiving |
|
Nov. 30 |
Quantum Trajectories I Introduction to measurment theory Master equation: quantum jump picture |
|
| Dec. 2 |
Quantum Trajectories II Quantum Monte-Carlo Wave Function Algorithm |
|
Dec. 7 |
Continuation: Multilevel Quantum Jumps |
|
Dec.
9 |
Quantum Trajectories III Different Unravelings of the Master Equation |
|
Additional Topics: Stochastic Schrödinger Equation Continuous Measurement |
Problem Set #1 |
Problem Set #4 |
Problem Set #2 |
Problem Set #5 |
Problem Set #3 |
Problem Set #6 |
Problem Set #7 |